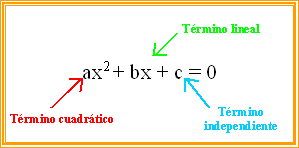Función cuadrática:

Fundamentación:

 

ü           Según el diseño curricular, hacer matemática es resolver problemas.

ü           La descontextualización de los resultados obtenidos es lo que permite generalizar y realizar transferencias pertinentes.

ü           El concepto de función es una de las nociones más importantes de la matemática. En esta propuesta se abordarán las funciones cuadráticas y se centra no sólo en la confección de tablas sino a partir de las discusiones sobre cuáles y cuántos son los puntos estratégicos para lograr ese gráfico.

ü           Además, es interesante reflexionar acerca de la información que la fórmula brinda en referencia a un gráfico.

ü           Se utilizarán recursos de la Web 2.0 para lograr una mejor comprensión del tema.

 

Contenidos previos:

 

ü           Operaciones en el conjunto de los números reales.

ü           Ubicación de puntos en el plano.

ü           Noción de función.

ü           Análisis de funciones.

ü           Función lineal.

ü           Uso de la calculadora.

ü           Uso de los recursos de la Web 2.0.

 

Objetivos de enseñanza:

 

ü           Promover el trabajo autónomo de los alumnos.

ü           Estimular la comprobación y validación de hipótesis mediante el uso de las herramientas matemáticas pertinentes.

ü           Promover la relación entre los contenidos nuevos y los que se hayan trabajado con anterioridad.

ü           Incorporar la enseñanza de la matemática a través de las nuevas tecnologías de la información y la conectividad.

 

Objetivos de aprendizaje:

 

ü           Construir conocimientos matemáticos significativos.

ü           Comprender la importancia de la formalización como herramienta de comunicación en el ámbito de la matemática.

ü           Resolver problemas modelizándolos a través de funciones cuadráticas.

ü           Identificar puntos notables.

ü           Analizar funciones.

ü           Interpretar el lenguaje matemático.

Inicio

 

En la antigüedad los griegos, desde antes de Euclides (330 – 275 AC) resolvían situaciones cuadráticas basándose en un método geométrico donde hacían intervenir cuadrados y rectángulos.

 En este caso nos dedicaremos al estudio de la función cuadrática, por medio de la cual es posible modelizar el comportamiento de fenómenos, tales como las curvas que describen las siguientes figuras:

 

La función cuadrática es una función polinómica que se define mediante un polinomio de segundo grado

 

Tiene la forma:

f(x) = ax2 + bx + c

Donde a, b y c son números reales cuales quieras y a distinto de cero.

 

Gráfico de la función cuadrática:

En la ecuación cuadrática sus términos se llaman:

• üSu forma depende del coeficiente a x2.
• Los coeficientes b y c trasladan la parábola a izquierda, derecha, arriba o abajo.
• Si a > 0 la parábola es cóncava o con sus ramas hacia arriba.
• Si a < 0 la parábola es convexa o con sus ramas hacia abajo.
• Cuanto más grande sea el valor absoluto de a, más cerrada es la parábola.
• Existe un único punto de corte al eje y, que es (0,c).

 

Concavidad y convexidad:

 

ü En las funciones cuadráticas podemos distinguir entre las que tienen concavidad positiva y las     que tienen concavidad negativa.

ü En ambas encontramos un punto extremo, llamado vértice, que puede ser el máximo o el mínimo de la función.

 

Raíces:

 

 Las raíces (o ceros) de la función cuadrática son aquellos valores de x para los cuales la expresión vale 0, es decir los valores de x tales que y = 0. Gráficamente corresponden a las abscisas de los puntos donde la parábola corta al eje x.

 

Ordenada al origen:

Es la coordenada en donde la parábola corta al eje y. Para encontrarla debemos calcular x = 0, es decir será el punto (0,c)

Eje de simetría:

Es la recta que divide simétricamente a la curva, es decir, la separa en dos partes congruentes. Este eje atraviesa el vértice

 

Cálculo de raíces y vértice:

Fórmulas para calcular raíces:

 

Fórmula para calcular el vértice:

 

Las funciones cuadráticas pueden o no tener raíces:

üPara resolver ecuaciones de segundo grado y saber si este tiene raíces hay un método que fue descubierto por Bháskara, un matemático Hindú.

üEn la fórmula aparece la raíz cuadrada del término b2-4.a.c. A este término se le llama discriminante, porque nos ayuda a discriminar si la función cuadrática tendrá o no raíces reales.

 

Observamos el discriminante:

 

 

Crecimiento y decrecimiento:

 

En el siguiente Powert point visualizaremos cómo graficar una función cuadrática utilizando excel

Función cuadrática: Excel from Horacio181

Ejercicio - Función cuadrática - Excel

Ejercicio - Función cuadrática - Excel from Horacio181

Mapa conceptual

A continuación, se presenta un mapa conceptual sobre la función cuadrática. El mismo fue realizado con la herramienta Cmap Tools.
Les brindo el enlace para poder utilizar esta aplicación:

Cmap Tools

 

Graficador de funciones on line

¿Cómo graficar y analizar funciones utilizando un software online?
Ingresa a la página de Wolfram Alpha e introduce los datos de tu función

Visualización de la trayectoria y de los cambios físicos que se producen al variar los parámetros

 

Para realizar esta actividad, deben descargar el archivo de GeoGebra, al que pueden acceder haciendo clic aquí.
El origen de las coordenadas se ubicó en el punto en el que se para el jugador para ejecutar el tiro libre, y las medidas respetan aproximadamente a las medidas reales.
Sus alumnos podrán variar las condiciones iniciales del tiro libre de básquet (altura, velocidad y ángulo de tiro) y visualizar cómo varía la trayectoria en función de ellos.

Después de variar las condiciones iniciales, y antes de iniciar el lanzamiento, es conveniente mover el deslizador “Pelota”, de manera que la pelota se ubique en el punto de partida (como se observa en la imagen). Ahora sí, activen la pelota con el botón , que se encuentra en el extremo inferior izquierdo de la pantalla.
Pueden ensayar varios tiros hasta lograr el enceste (pueden estimar las posiciones iniciales, considerando qué parámetros pueden variar si necesitan, por ejemplo, que la curva sea más “cerrada”, o si es preciso que la pelota alcance mayor altura, etcétera).
Si quieren borrar las trayectorias anteriores, alcanza con presionar Ctrl + F.
También pueden buscar en Internet la altura de algunos basquetbolistas famosos e intentar distintas velocidades y ángulos de tiro hasta encestar. Además, podrían indicarles distintas condiciones iniciales y pedirles que hallen la posición de la pelota al alcanzar la altura máxima en ese tiro, o el alcance de ella, en el caso de no encestar. Se muestran dos ejemplos:
Si la pelota parte desde una altura de 2,05 m con un ángulo de 50º y una velocidad de 7,30 m/s, ¿cuál será la posición de la pelota al alcanzar la altura máxima?
Si ahora la pelota parte desde una altura de 2,30 m con un ángulo de 60º y una velocidad de 6,8 m/s, ¿a qué distancia del jugador la pelota tocará el piso (a esta distancia se la llama alcance)?
Para verificar las soluciones obtenidas, sus alumnos podrán ubicar los deslizadores según las condiciones del problema y tildar las casillas correspondientes en el mismo archivo. Los deslizadores también pueden usarse haciendo clic sobre cada uno y moviéndolos con las flechas del teclado.
Igualmente pueden incluirse problemas en los que se dan algunas de las posiciones iniciales y se buscan otras, como: en el último partido, Juan lanzó un tiro libre y la pelota alcanzó la máxima altura al ubicarse en el (2,83; 4). Cuando realizó el lanzamiento, Juan soltó la pelota a 1,90 m del piso y con un ángulo de tiro de 56º. ¿Con qué velocidad lanzó la pelota?
Como en los problemas anteriores, la respuesta puede verificarse en el mismo archivo, pero esta vez se deberán mover los deslizadores hasta los valores que se dieron como dato y hasta la velocidad obtenida, y verificar el punto donde se alcanza la altura máxima. (Es aconsejable trabajar con todos los decimales de la calculadora para no propagar errores, y redondear los centésimos solo en la respuesta).

Fuente: www.educ.ar

GeoGebra

En el siguiente enlace podemos acceder al GeoGebra online
https://www.geogebra.org/webstart/geogebra.html

Aplicaciones de la Funcion Cuadratica

HIPERTEXTO

Función cuadrática

 

Noriega, Horacio

horacionoriega@hotmail.com

 

Es toda función  cuya expresión polinómica de segundo grado es de la forma:

Donde a, b y c son números reales cuales quieras y a distinto de cero.

 

El gráfico de una función cuadrática  es una curva llamada parábola.

En la ecuación cuadrática sus términos se llaman:

 

 

ü      Su forma depende del coeficiente a x².

ü      Los coeficientes b y c trasladan la parábola a izquierda, derecha, arriba o abajo.

 

Concavidad y convexidad:

ü      En las funciones cuadráticas podemos distinguir entre las que tienen concavidad positiva y las que tienen concavidad negativa.

ü      En ambas encontramos un punto extremo, llamado vértice, que puede ser el máximo o el mínimo de la función.

ü      Si a > 0, la parábola es cóncava hacia arriba; si a < 0, es cóncava hacia abajo.

ü      Cuanto más grande sea el valor absoluto de a, más cerrada es la parábola.

ü      Existe un único punto de corte al eje y, que es (0,c).

 

Raíces:

Las raíces (o ceros) de la función cuadrática son aquellos valores de x para los cuales la expresión vale 0, es decir los valores de x tales que y = 0. Gráficamente corresponden a las abscisas de los puntos donde la parábola corta al eje x.

Una forma práctica de encontrar las raíces es aplicar la fórmula resolvente de Bháskara.

Ordenada al origen:

Es la coordenada en donde la parábola corta al eje y. Para encontrarla debemos calcular f(0), o sea, es el valor que toma  y cuando x = 0.

Si la función está expresada en forma polinómica la ordenada al origen será el punto (0,c).

 

Eje de simetría:

Es la recta que divide simétricamente a la curva, es decir, la separa en dos partes congruentes. Se puede hallar empleando la siguiente fórmula.

 

 Vértice:

Es el punto del eje de simetría en el que la función pasa de decreciente a creciente, o viceversa. Por lo tanto, la ordenada del vértice y_v, es el mínimo o el máximo de la función.
 

La coordenada del vértice estará dada por:

                                                                        V = (Xv; F(Xv))

 

Las funciones cuadráticas pueden o no tener raíces:

ü      Para resolver ecuaciones de segundo grado y saber si este tiene raíces hay un método que fue descubierto por Bháskara, un matemático Hindú.

ü      En la fórmula aparece la raíz cuadrada del término b²-4.a.c. A este término se le llama discriminante, porque nos ayuda a discriminar si la función cuadrática tendrá o no raíces reales.

 

Ejemplos:

 

Ø      Gráfico de función cuadrática.

 

Ø      Aplicación de la función cuadrática.

 

Ø      Calculadora para el estudio de la función cuadrática.