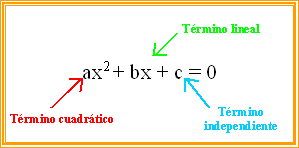GeoGebra

En el siguiente enlace podemos acceder al GeoGebra online
https://www.geogebra.org/webstart/geogebra.html

Aplicaciones de la Funcion Cuadratica

HIPERTEXTO

Función cuadrática

 

Noriega, Horacio

horacionoriega@hotmail.com

 

Es toda función  cuya expresión polinómica de segundo grado es de la forma:

Donde a, b y c son números reales cuales quieras y a distinto de cero.

 

El gráfico de una función cuadrática  es una curva llamada parábola.

En la ecuación cuadrática sus términos se llaman:

 

 

ü      Su forma depende del coeficiente a x².

ü      Los coeficientes b y c trasladan la parábola a izquierda, derecha, arriba o abajo.

 

Concavidad y convexidad:

ü      En las funciones cuadráticas podemos distinguir entre las que tienen concavidad positiva y las que tienen concavidad negativa.

ü      En ambas encontramos un punto extremo, llamado vértice, que puede ser el máximo o el mínimo de la función.

ü      Si a > 0, la parábola es cóncava hacia arriba; si a < 0, es cóncava hacia abajo.

ü      Cuanto más grande sea el valor absoluto de a, más cerrada es la parábola.

ü      Existe un único punto de corte al eje y, que es (0,c).

 

Raíces:

Las raíces (o ceros) de la función cuadrática son aquellos valores de x para los cuales la expresión vale 0, es decir los valores de x tales que y = 0. Gráficamente corresponden a las abscisas de los puntos donde la parábola corta al eje x.

Una forma práctica de encontrar las raíces es aplicar la fórmula resolvente de Bháskara.

Ordenada al origen:

Es la coordenada en donde la parábola corta al eje y. Para encontrarla debemos calcular f(0), o sea, es el valor que toma  y cuando x = 0.

Si la función está expresada en forma polinómica la ordenada al origen será el punto (0,c).

 

Eje de simetría:

Es la recta que divide simétricamente a la curva, es decir, la separa en dos partes congruentes. Se puede hallar empleando la siguiente fórmula.

 

 Vértice:

Es el punto del eje de simetría en el que la función pasa de decreciente a creciente, o viceversa. Por lo tanto, la ordenada del vértice y_v, es el mínimo o el máximo de la función.
 

La coordenada del vértice estará dada por:

                                                                        V = (Xv; F(Xv))

 

Las funciones cuadráticas pueden o no tener raíces:

ü      Para resolver ecuaciones de segundo grado y saber si este tiene raíces hay un método que fue descubierto por Bháskara, un matemático Hindú.

ü      En la fórmula aparece la raíz cuadrada del término b²-4.a.c. A este término se le llama discriminante, porque nos ayuda a discriminar si la función cuadrática tendrá o no raíces reales.

 

Ejemplos:

 

Ø      Gráfico de función cuadrática.

 

Ø      Aplicación de la función cuadrática.

 

Ø      Calculadora para el estudio de la función cuadrática.